Generative Adversarial Nets

论文名称

Generative Adversarial Nets
会议:NIPS2014

摘要

提出一个framework通过对抗的过程，估计生成的模型：同时训练两个模型。

一个生成模型G:抓住整个数据的分布，生成和原始数据相似的数据，G的训练过程最大化D犯错的概率。 一个辨别模型D:辨别一个数据是来自真实训练集，还是来自G生成的数据。

在任何函数空间的G和D，有一个独一无二的解，G能挖掘出原始数据分布，使D的预测概率为$\frac{1}{2}$.

Introduction

深度学习是发现丰富的、有层次的模型可以对各种AI应用的数据做出概率分布的表示。深度学习已经对辨别模型，取得了很大的进展，但是在生成模型上还有很大发展空间。这主要由于最大化似然函数，需要对概率分布近似，带来了计算上的困难，并且难以再生成上下文中利用分段线性单元的优势。

作者提出了对抗生成网络框架，生成模型与辨别模型对抗，辨别模型能够辨别数据的来源是生成模型或者原始数据分布，生成模型能够生成和原始数据相似的伪造物。

作者举了个例子，生成模型用于伪造货币并使用它，而辨别模型就像警察，辨认出伪造的货币。他们会改进他们的方法，直到伪造物难以与真正的数据中辨认。

Related work

大部分深度生成模型的工作集中在概率分布函数的参数化模型上，这些模型可以使用最大化对数似然函数训练，在这些模型中，最成功的或许是深度玻尔兹曼机，这些模型都有着难以计算的似然函数，需要对似然函数近似。

生成随机网络是一个能够使用反向传播训练的模型，而不是许多的近似。它通过消除生成随机网络中使用的马尔科夫链来扩展生成模型的思想。

Adversarial nets

对抗模型框架可以在模型都是MLP时直接使用。

定义generator在数据$x$上的分布$p_{g}$，noise的分布为$p_{z}(z)$，将数据空间的映射表示为$G(z;{\theta}_{g})$，其中$G$时可微函数，由参数为${\theta}_{g}$的多层感知器表示。
定义第二个感知器$D(x;{\theta}_{d})$，其输出为单个标量。$D(x)$表示$x$来自原始数据而不是$p_{g}$的概率。

训练$D$以最大限度的提高将正确标签分配给训练样本和来自$G$的样本。同时训练$G$最小化$log(1-D(G(z)))$，即$D$和$G$遵循如下函数:

$${\min\limits_{G}}{\max\limits_{D}}V(D,G)=\mathbb{E}_{x{\sim}p_{data}(x)}[{\log}D(x)]+\mathbb{E}_{z{\sim}p_{z}(z)}[\log(1-D(G(z)))]$$

$G$和$D$有能力去恢复数据的分布。下图是对该方法的一个解释。

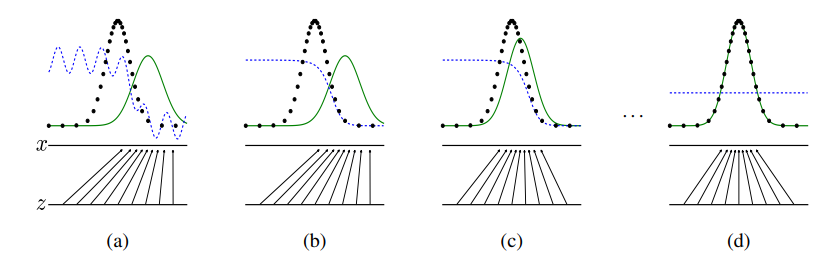
生成对抗网络通过同时更新判别性分布(D，蓝色，虚线)，使其对数据生成分布(黑色，虚线)$p_{x}$的样本和生成分布$p_{g}(G)$(绿色，实线)的样本进行区分。下方的水平线是$z$的取样域，在这种情况下是均匀的。上方的水平线是$x$域的一部分。向上的箭头显示了映射$x=G(z)$是如何将非均匀分布$p_{g}$转换。$G$在$p_{g}$的高密度区域收缩，在低密度区域扩张。(a)考虑一个接近收敛的对抗对:$p_{g}$与$p_{data}$相似，D是一个部分准确的分类器。(b)在算法的内循环中，$D$被训练成从数据中辨别样本，收敛到$D^{*}(x)=\frac{p_{data}(x)}{p_{data}(x)+p_{g}(x)}$. (c)在对$G$进行更新后，$D$的梯度引导$G(z)$流向更有可能被列为数据的区域。被归类为数据的区域。(d)经过几步训练，如果G和D有足够的能力，它们将达到一个点，因为$p_{g}=p_{data}$，$D$无法区分两种分布，即$D(x)=\frac{1}{2}$.

在实践中，训练的内循环中对$D$优化一方面计算量较大，另一方面容易导致过拟合。使用优化$D$的k次和优化$G$一次交替运行，只要$G$的变化足够慢，$D$就能保持在其最优解附近。如下图算法描述:

在实践中，上述方程可能无法为$G$提供足够的梯度使其训练好，在学习的早期，由于$G$的效果很差，因此可以很有把握的拒绝样本，因为$G$生成数据明显和原始数据不同，这种情况下，$\log(1-D(G(z)))$会达到饱和。与其训练$G$去最小化$log(1-D(G(z)))$，不如训练$G$去最大化$log(D(G(z)))$。这个目标函数在学习早期提供了更大的梯度。

Theoretical Results

生成器$G$隐含地定义了一个概率分布$p_{g}$，作为样本的分布$G(z)$，当$z{\sim}p_{z}$时得到。因此，如果有足够的容量和训练时间，我们希望算法1能收敛到一个好的估计。

本节的结果是在非参数设置下完成的，通过研究概率密度函数空间的收敛性来表示一个具有无限容量的模型。

Global Optimality of $p_{g}=p_{data}$

首先考虑优化分辨器$D$对任意的生成器$G$。

• Proposition 1. 对于给定的$G$，辨别模型$D$的最优为

$$D^{*}_{G}(x)=\frac{p_{data}(x)}{p_{data}(x)+p_{g}(x)}$$

证明: 在给定任何生成模型$G$的情况下，判别器D的训练标准是最大化$V(G,D)$

$$V(G,D)={\int}_{x}p_{data}(x){\log(D(x))}dx + {\int_{z}p_{z}(z)\log(1-D(g(z)))dz}$$

$$V(G,D)={\int_{x}p_{data}(x)\log(D(x))+p_{g}(x)\log(1-D(x))dx}$$

对于${\forall}(a,b){\in}\mathbb{R}^{2}/(0,0)$，函数$y{\rightarrow}a{\log(y)}+b{\log(1-y)}$当$y=\frac{a}{a+b}{\in}[0,1]$时有最值。

D的训练目标可以解释为最大化估计条件概率$P(Y = y|x)$的对数可能性，其中$Y$表示$x$是否来自$p_{data}(y=1)$或$p_{g}(y=0)$。公式1中的minmax现在可以重新表述为:

$$C(G)=\max\limits_{D}V(G,D)$$

$$C(G)=\mathbb{x{\sim}p_{data}}[{\log}D^{*}_{G}(x)]+\mathbb{x{\sim}p_{data}}[1-{\log}D^{*}_{G}(G(z))]$$

$$C(G)=\mathbb{x{\sim}p_{data}}[{\log}D^{*}_{G}(x)]+\mathbb{x{\sim}p_{g}}[1-{\log}D^{*}_{G}(x)]$$

$$C(G)=\mathbb{x{\sim}p_{data}}[{\log}\frac{p_{data}(x)}{p_{data}(x)+p_{g}(x)}]+\mathbb{x{\sim}p_{g}}[\log\frac{p_{g}(x)}{p_{data}(x)+p_{g}(x)}]$$

• Theorem 1.当且仅当$p_{g}=p_{data}$，$C(G)$达到全局最小值。在这一点上，$C(G)$达到的数值是$-{\log4}$ 证明: $p_{g}=p_{data}$，$D^{*}_{G}(x)=\frac{1}{2}$(Proposition 1)，$C(G)=\log{\frac{1}{2}}+\log{\frac{1}{2}}=-\log{4}$，为了说明这是$C(G)$的最佳可能值，只在$p_{g}=p_{data}$时达到的最佳值，需要注意

$$\mathbb{E}_{x{\sim}p_{data}}[-\log{2}]+\mathbb{E}_{x{\sim}p_{y}}[-\log{2}]=-\log{4}$$

从$c(G)=V(D^{*}_{G},G)$中减去这个表达式，可得

$$C(G)=-\log{4}+KL\begin{pmatrix}p_{data}{\lvert}{\rvert}\frac{p_{data}+p_{g}}{2}\end{pmatrix}+KL\begin{pmatrix}p_{g}{\lvert}{\rvert}\frac{p_{data}+p_{g}}{2}\end{pmatrix}$$

其中$KL$为KL散度，在前面的表达中认识到模型的分布和数据生成过程之间的JS散度。

$$C(G)=-\log{(4)}+2{\cdot}JSD(p_{data}||p_{g})$$

由于两个分布之间的JS散度总是非负的，并且在它们相等的情况下为零。如果它们相等，我们已经证明$C^{*}=-\log(4)$是$C(G)$的全局最小值，并且唯一的解是$p_{g} =p_{data}$，也就是说，生成模型完全复制了数据分布。

算法1的收敛

• Proposition 2 如果$G$和$D$有足够的能力，并且在算法1的每一步，判别器被允许达到其最佳状态，并且$p_{g}$被更新，以提高标准

$$\mathbb{E}_{x{\sim}p_{data}}[{\log}D^{*}_{G}(x)]+\mathbb{E}_{x{\sim}p_{g}}[\log(1-D^{*}_{G}(x))]$$

那么$p_{g}$收敛到$p_{data}$

证明:考虑$V(G,D)=U(p_{g},D)$作为上述标准中的$p_{g}$的函数。注意$U(p_{g},D)$在$p_{g}$中是凸的。凸函数的最高值的子导数包括函数在达到最大时的导数。凸函数最高值的子导数包括函数在达到最大值的那一点的导数。换言之，如果$f(x)=\sup_{\alpha\in\mathcal{A}}f_{\alpha}(x)$，且$f_{\alpha}(x)$在$x$中对每个$\alpha$都是凸的，那么如果$\beta=\arg\sup_{\alpha\in\mathcal{A}f_{\alpha}(x)}$,则${\partial}f_{\beta}(x)\in{\partial}f$.这相当于在给定相应$G$的情况下，在最优$D$处计算$p_{g}$的梯度下降更新。$\sup_{D}U(p_{g},D)$在$p_{g}$中是凸的，有一个唯一的全局最优，这在问题1中已经证明。因此，在对$p_{g}$进行足够小的更新时，$p_{g}$会收敛到$p_{x}$，从而结束了这个证明。
在实践中，对抗网络通过函数$G(z;\theta_{g})$代表了一个有限的$p_{g}$分布系列，而我们优化的是$\theta_{g}$而不是$p_{g}$本身，所以这些证明并不适用。然而，多层感知器在实践中的出色表现表明，尽管它们缺乏理论保证，但它们是一个合理的模型，可以使用。

Experiments

实验主要基于MNIST、TFD、CIFAR10。

生成模型使用了sigmoid和ReLU激活函数，而判别模型使用了maxout激活函数。在训练辨别模型时使用了Dropout。虽然理论框架允许在生成模型的中间层使用dropout和其他噪声，但我们只将噪声作为输入到生成器网络的最底层。

优势和劣势

优点

• 不需要马尔科夫链。
• 学习过程中不需要推理，而且各种各样的函数都可以纳入模型中。

缺点

没有明确表示$p_{g}(x)$，而且$D$必须在训练过程中与$G$同步(特别是，$G$不能在没有更新$D$的情况下训练太多以避免出现 "Helvetica情况"，即$G$将太多的$z$值折叠成相同的$x$值。