RNN

一、RNN的几种基本的结构

1.1 结构一

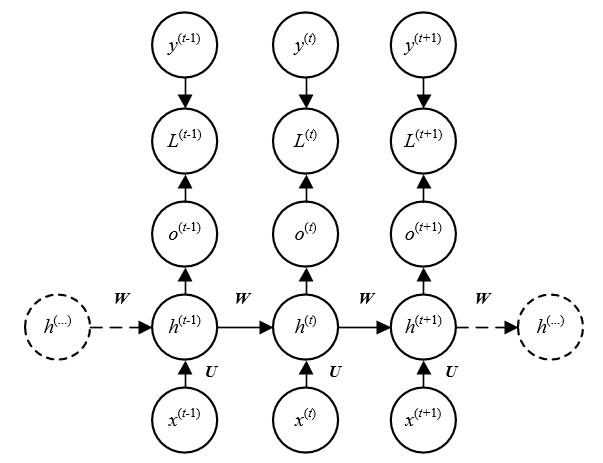
上述所示RNN的结构中，输入序列为$X=(x^{0},x^{1},...,x^{l-1})$。对于任意时刻$t$，$h^{t}$由$h^{t-1}$和$x^{t}$共同决定。且目标时刻$t$对应于目标输出$y^{t}$。这样的结构很适合时间序列类预测的任务，模型可以通过之前的信息$h^{t-1}$和当前的输入$x_{t}$来预测当前时刻的输出$\hat{y}^{t}$。该结构最大的问题是时刻$t$的损失$L^{t}$与所有之前的状态$h^{t-1}$,$h^{t-2}$,...,$h^{0}$都有关系。因此求$h^{t}$时，要先求$h^{t-1}$。在反向传播时，需要对每一个输入进行前向传播过程来计算网络的activation，而RNN的顺序计算，会导致难以并行化，导致训练较慢。

1.2 结构二

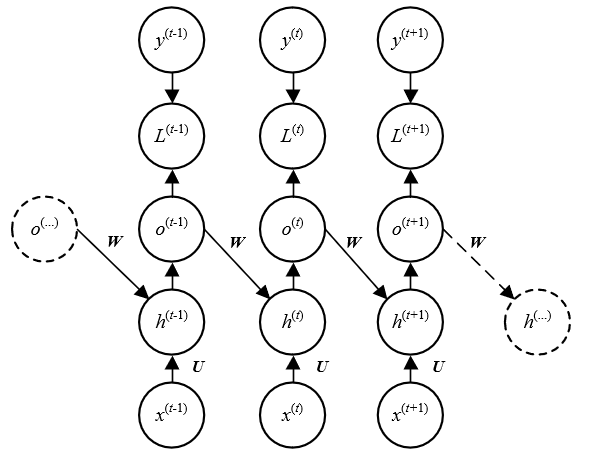
与结构一相比，这种结构取消了相邻时刻间状态$h$之间的连接，取而代之的是前一时刻的输出$o^{t-1}$与当前时刻状态$h^{t}$的连接，此时仍然是顺序计算，但$o$的维度通常小于$h$，因此训练参数可能减少。模型的缺点主要是$y^{t}$中的信息远少于$h^{t}$，因此模型对历史信息的学习能力不如结构一。

这种网络可以采用teacher forcing的方法来训练，$h^{t}$的输入部分来自$o^{t-1}$，而$o^{t-1}$本身在训练过程中受$y^{t-1}$的约束($o^{t-1}$要尽可能逼近$y^{t-1}$)，因此可以直接使用$y^{t-1}$来代替$o^{t-1}$作为$h^{t}$的输入。

1.3 结构三

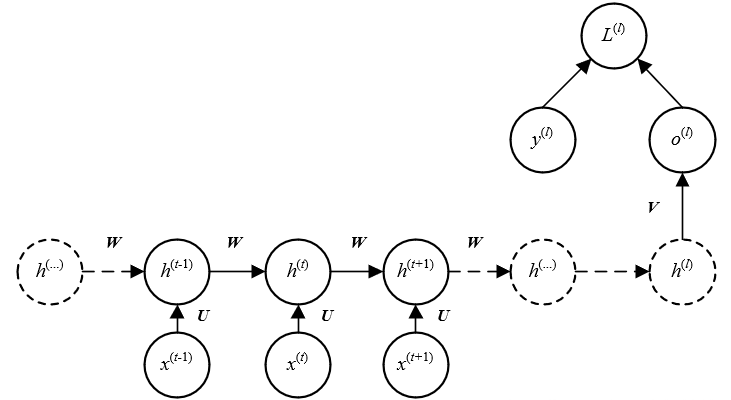
该结构的RNN仅在最后时刻$l$才会有输出$o^{l}$。

二、前向传播

2.1 理论推导

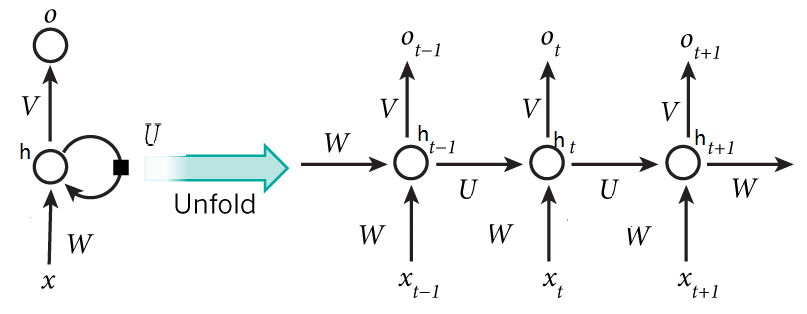
定义完全连接的循环神经网络，输入为$x_{t}$，输出为$y_{t}$。

$$h_{t}=f(Uh_{t-1}+Wx_{t}+b)$$

$$y_{t}=Vh_{t}$$

提示

其中$h$为隐状态，$f(\cdot)$为非线性激活函数，通常使用Logisitic函数或Tanh函数，$U$、$W$、$b$和$V$为网络参数。

$x_{t}{\in}{\mathcal{R}^{M}}$表示时刻t网络的输入，$h_{t}{\in}{\mathcal{R}^{D}}$表示隐藏层状态，$U{\in}{\mathcal{R}}^{D{\times}D}$表示状态-状态权重矩阵，$W{\in}{\mathcal{R}}^{D{\times}M}$表示状态-输入权重矩阵，$b{\in}{\mathcal{R}}^{D}$表示偏置向量。

若将每个时刻的状态都看作前馈神经网络的一层，循环神经网络可以看作在时间维度上权值共享的神经网络。

2.2 代码实现

使用矩阵的推导。

def get_params(embedding_size, output_size, num_hiddens, device):
    """
    获取RNN的参数

    Args:
        embedding_size: 词嵌入的维度
        output_size: 输出的维度
        num_hiddens: 隐藏层大小
        device: 训练设备
    
    Returns:
        参数的元组
    """
    # 输入的维度假设为词嵌入的维度
    num_inputs = embedding_size
    # 输出的维度假设为output_size
    num_outputs = output_size
    # 使用正态分布初始化权重
    def normal(shape):
        return torch.randn(size=shape, device=device) * 0.1
    # 隐藏层的参数
    W = normal((num_inputs, num_hiddens))
    U = normal((num_hiddens, num_hiddens))
    b_h = torch.zeros(num_hiddens, device=device)
    # 输出层参数
    V = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    # 附加梯度
    params = [W, U, b_h, V, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

三、应用模式

3.1 序列到类别模式

提示

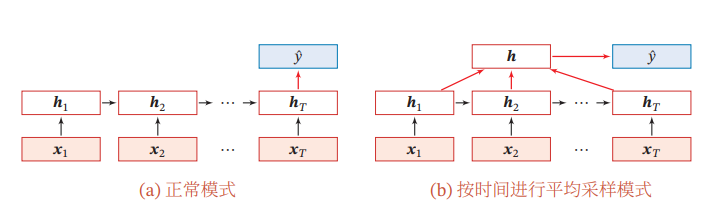
主要用于序列数据的分类：输入数据为序列，输出为类别。

输入的样本$x_{1:T}=(x_{1},...,x_{T})$为一个长度为T的序列，输出类别$y{\in}{\{}1,...,C{\}}$，将样本$x$，按不同时刻输入到循环神经网络中，得到不同时刻的隐藏状态$h_{1},...,h_{T}$，可以将$h_{T}$看作整个序列的最终表示，并输入给分类器$g(\cdot)$进行分类。

如上图所示，除了使用最后时刻的状态作为整个序列的表示，也可以使用整个状态的所有状态进行平均，并使用这个平均状态作为整个序列的表示，即$\hat{y}=g(\frac{1}{T}\sum\limits_{t=1}^{T}h_{t})$

3.2 同步的序列到序列模式

提示

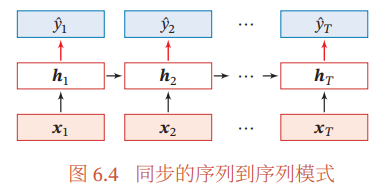
主要用于序列标注任务，即每一时刻都有输入和输出，输入序列和输出序列的长度相同。

输入的样本$x_{1:T}=(x_{1},...,x_{T})$为一个长度为T的序列，输出为序列$y_{1:T}=(y_{1},...,y_{T})$。将样本$x$，按不同时刻输入到循环神经网络中，得到不同时刻的隐藏状态$h_{1},...,h_{T}$，每个时刻的隐状态$h_{t}$代表了当前时刻的和历史的信息，并输入给分类器$g(\cdot)$得到当前时刻的标签$\hat{y}$，即$\hat{y}_{t}=g(h_{t}), \forall{t}{\in}[1,T]$.

3.3 异步的序列到序列模式

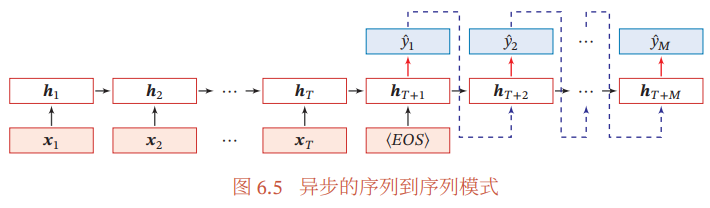
令$f_{1}(\cdot)$和$f_{2}(\cdot)$分别为编码器和解码器的循环神经网络，则编码器-解码器模型可以写为:

$$h_{t}=f_{1}(h_{t-1},x_{t}),{\forall}t{\in}[1,T]$$

$$h_{T+t}=f_{2}(h_{T+t-1},\hat{y}_{t-1}),{\forall}t{\in}[1,M]$$

$$\hat{y}_{t}=g(h_{T+t}),{\forall}t{\in}[1,M]$$

其中$g(\cdot)$为分类器，$\hat{y}_{t}$为预测输出$\hat{y}_{t}$的向量表示。 在解码器通常采用自回归模型，每个时刻的输入为上一时刻的预测结果$\hat{y}_{t-1}$。如上图所示，其中$<EOS>$表示输入序列的结束，虚线表示将上一时刻的输出作为下一时刻的输入。

提示

异步的序列到序列模式也称为编码器-解码器模型。即输入序列和输出序列不需要严格的对应关系，也不需要保持相同的长度，例如机器翻译任务。

输入的样本$x_{1:T}=(x_{1},...,x_{T})$为一个长度为T的序列，输出为长度为M的序列$y_{1:M}=(y_{1},...,y_{M})$。

异步的序列到序列模式一般通过先编码后解码的方式来实现，先将样本$x$按不同时刻输入到一个循环神经网络(编码器)中，得到其编码$h_{T}$，然后再使用另一个循环神经网络(解码器)，得到输出序列$\hat{y}_{1:M}$。为了建立输出序列之间的依赖关系，再解码器中通常使用非线性的自回归模型。

四、参数学习

循环神经网络的参数可以通过梯度下降的方法来进行学习。

以随机梯度下降为例，给定一个训练样本$(x,y)$，其中$x_{1:T}=(x_{1},...,x_{T})$为长度是$T$的输入序列，$y_{1:T}=(y_{1},...,y_{T})$是长度为$T$的标签序列，每个时刻$t$都有一个监督信息$y_{t}$，我们定义时刻$t$的损失函数为

$$\mathcal{L}_{t}={\mathcal{L}}(y_{t},g(h_{t}))$$

其中$g(h_{t})$为第$t$时刻的输出，$\mathcal{L}$为可微分的损失函数，如交叉熵等，整个序列的损失函数为

$$\mathcal{L}=\sum_{t=1}^{T}{\mathcal{L}}_{t}$$

则整个序列的损失函数$\mathcal{L}$关于参数$U$的梯度为

$$\frac{\partial{\mathcal{L}}}{\partial{U}}={\sum_{t=1}^{T}{\frac{\partial{\mathcal{L}_{t}}}{\partial{U}}}}$$

即每个时刻损失$\mathcal{L}_{t}$对参数$U$的偏导数之和。

BPTT和RTRL比较:在循环神经网络中，一般网络输出维度要远低于输入维度，因此BPTT算法的计算量会小，但是BPTT算法需要保存中间所有时刻的中间梯度，空间复杂度高。RTRL算法不需要梯度回传，因此非常适用于需要在线学习或无限序列的任务中。

4.1 随时间反向传播算法 BPTT

算法主要思想:通过类似前馈神经网络的误差反向传播算法来计算梯度。

BPTT算法将循环神经网络看作一个展开的多层前馈网络，其中“每一层”对应循环网络中的“每个时刻”。这样，循环神经网络可以按照前馈神经网络中的反向传播算法计算参数梯度。在“展开”的前馈神经网络中，所有层的参数是共享的，因此参数的真实梯度是所有“展开层”的参数梯度之和。

计算偏导数$\frac{\partial{\mathcal{L}_{t}}}{U}$:首先计算第$t$时刻损失对参数$U$的偏导数。
因为参数$U$和隐藏层在每个时刻$k(1{\leq}k{\leq}t)$的净输入$z_{k}=Uh_{k-1}+Wx_{k}+b$有关(根据前向传播计算公式)，因此$t$时刻的损失函数$\mathcal{L}_{t}$关于参数$u_{ij}$的梯度为(链式法则):

$${\frac{\partial{L_{t}}}{u_{ij}}}=\sum_{k=1}^{t}{\frac{\partial{^{+}z_{k}}}{\partial{u_{ij}}}\frac{\partial{L_{t}}}{\partial{z_{k}}}}$$

其中$\frac{\partial{^{+}z_{k}}}{\partial{u_{ij}}}$为直接偏导数，即$z_{k}=Uh_{k-1}+Wx_{k}+b$中$h_{k-1}$保持不变，对$u_{ij}$求偏导数，得到

$$\frac{\partial{^{+}z_{k}}}{\partial{u_{ij}}}=[0,...,[h_{k-1}]_{j},...,0]$$

其中$[h_{k-1}]_{j}$为第$k-1$时刻隐状态的第$j$维。
定义误差项${\delta_{t,k}}=\frac{\partial{L_{t}}}{\partial{z_{k}}}$为第$t$时刻的损失对第$k$时刻隐藏层神经层的净输入$z_{k}$的导数，则当$1{\leq}k<t$时

$${\delta_{t,k}}=\frac{\partial{\mathcal{L}_{t}}}{\partial{z_{k}}}=\frac{\partial{h_{k}}}{\partial{z_{k}}}\frac{\partial{z_{k+1}}}{\partial{h_{k}}}\frac{\partial{L_{t}}}{\partial{z_{k+1}}}$$

因此有

$${\delta_{t,k}}=diag(f^{'}(z_{k}))U^{T}{\delta_{t,k+1}}$$

将${\delta_{t,k}}$、$\frac{\partial{^{+}z_{k}}}{\partial{u_{ij}}}$代入到${\frac{\partial{L_{t}}}{u_{ij}}}$中得到

$${\frac{\partial{L_{t}}}{u_{ij}}}=\sum_{k=1}^{t}[\delta_{t,k}]_{i}[h_{k-1}]_{j}$$

写成矩阵形式有

$$\frac{\partial{\mathcal{L_{t}}}}{U}=\sum_{k=1}^{t}{\delta_{t,k}}h_{k-1}^{T}$$

代入到$\frac{\partial{\mathcal{L}}}{\partial{U}}$，得到整个序列的损失函数$\mathcal{L}$关于参数$U$的梯度

$$\frac{\partial{\mathcal{L}}}{\partial{U}}=\sum_{t=1}^{T}\sum_{k=1}^{t}\delta_{t,k}h_{k-1}^{T}$$

同理可得$\mathcal{L}$关于权重$W$和偏置$b$的梯度为

$$\frac{\partial{\mathcal{L}}}{\partial{W}}=\sum_{t=1}^{T}\sum_{k=1}^{t}\delta_{t,k}x_{k}^{T}$$

$$\frac{\partial{\mathcal{L}}}{\partial{b}}=\sum_{t=1}^{T}\sum_{k=1}^{t}\delta_{t,k}$$

$$$$

误差随时间进行反向传播算法的示例:

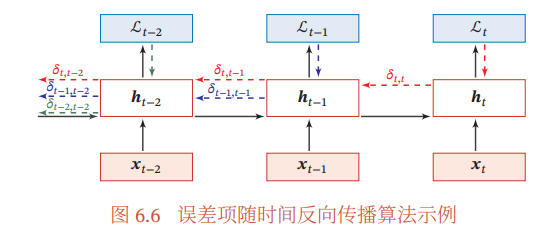
由上述推导过程可知，在BPTT算法中，参数的梯度需要在一个完整的“前向”计算和“反向”计算后才能得到并进行参数更新。

4.2 实时循环学习算法 RTRL

实时循环学习通过前向传播的方式来计算梯度。
假设循环神经网络中第$t$时刻的状态为$h_{t+1}$为

$$h_{t+1}=f(z_{t+1})=f(Uh_{t}+Wx_{t+1}+b)$$

其中关于参数$u_{ij}$的偏导数为

$$\frac{\partial{h_{t+1}}}{\partial{u_{ij}}}=(\frac{\partial{^{+}z_{t+1}}}{\partial{u_{ij}}}+\frac{\partial{h_{t}}}{\partial{u_{ij}}}U^{T})\frac{\partial{h_{t+1}}}{\partial{z_{t+1}}}$$

$$\frac{\partial{h_{t+1}}}{\partial{u_{ij}}}=(\frac{\partial{^{+}z_{t+1}}}{\partial{u_{ij}}}+\frac{\partial{h_{t}}}{\partial{u_{ij}}}U^{T})diag(f'(z_{t+1}))$$

RTRL算法从第1个时刻开始，除了计算循环神经网络的隐状态之外，还依次前向计算偏导数$\frac{\partial{h_{1}}}{\partial{u_{ij}}}$,$\frac{\partial{h_{2}}}{\partial{u_{ij}}}$,$\frac{\partial{h_{3}}}{\partial{u_{ij}}}$,...
假设在第$t$时刻存在一个监督信息，其损失函数为$\mathcal{L}_{t}$，可以同时计算损失函数对$u_{ij}$的偏导数

$$\frac{\partial{\mathcal{L}_{t}}}{\partial{u_{ij}}}=\frac{\partial{h_{t}}}{\partial{u_{ij}}}\frac{\partial{\mathcal{L}_{t}}}{\partial{h_{t}}}$$

这样可以在$t$时刻，实时计算损失$\mathcal{L}_{t}$关于参数$U$的梯度，并更新参数。参数$W$和$b$同样按上述方法实时计算。

参考文献

[1] 邱锡鹏，神经网络与深度学习，机械工业出版社，https://nndl.github.io/, 2020.
[2] 深度学习（三）：详解循环神经网络RNN，含公式推导
[3] 动手学深度学习
[4] 零基础入门深度学习(5) - 循环神经网络