Controllable Text Generation with Neurally-Decomposed Oracle

论文名称

Controllable Text Generation with Neurally-Decomposed Oracle

会议: NIPS2022

Abstract

我们提出了一个通用的、高效的框架，用NeurAlly-Decomposed Oracle（NADO）控制自动回归生成模型。给定一个预先训练好的基础语言模型和一个序列级的布尔oracle函数，我们建议将oracle函数分解为token级的指导，以引导文本生成中的基础模型。具体来说，token级引导由一个用基础模型采样的例子训练的神经模型来近似，不需要额外的辅助标记数据。我们提出了封闭式的最佳解决方案，将token级引导纳入可控生成的基础模型。我们进一步提供了关于NADO的近似质量如何影响可控生成结果的理论分析。在两个应用中进行的实验：(1)带有词汇约束的文本生成和(2)带有形式控制的机器翻译，表明我们的框架能有效地引导基础模型向给定的oracle前进，同时保持高的生成质量。

1 Introduction

自动回归语言模型已被广泛用于文本生成。随着最近大规模预训练语言模型的发展Radford等人（2019）；Brown等人（2020）；Raffel等人（2020）；Lewis等人（2020），他们在机器翻译（Bahdanau等人。2015；Luong等人，2015）、图像字幕（Anderson等人，2018；You等人，2016）和开放域文本生成（Zhang和Lapata，2014；Yao等人，2019；Vinyals和Le，2015；Shang等人，2015；Lu等人，2018）。然而，许多应用需要用特定的序列级属性来控制模型输出。这些属性可以由一组规则或一个抽象的概念（例如，生成的文本遵循特定的写作风格）来指定。如何控制自动回归语言模型以满足这些属性是一个公开的挑战。

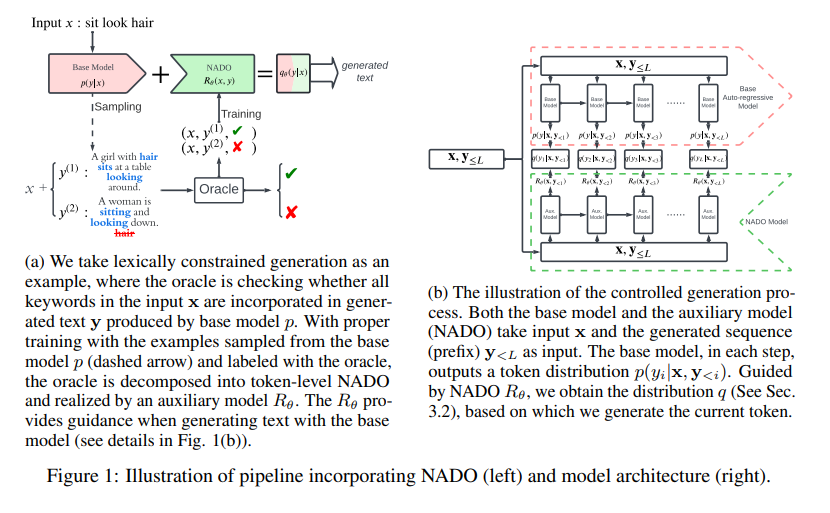
在本文中，我们提出了一个通用的、灵活的可控生成框架。给定一个基础的预训练语言模型和一个表明是否满足某个属性的序列级oracle函数，我们的目标是通过神谕引导文本生成以满足某些属性。为此，我们建议将序列级属性分解为token级引导。当在输出序列中生成第i个标记时，我们不是从给定前缀的基础模型中取样，而是根据token级引导来修改输出标记的概率分布。具体来说，我们将控制制定为一个基于后验正则化的优化问题（Ganchev等人，2010），并解决近似形式的最优解，以纳入文本生成的token级指导。分解由一个辅助的神经网络模型近似，称为NeurAlly-Decomposed Oracle（NADO），它是在从基础模型采样的数据上训练的，并由序列级神谕监督（见图1a的说明）。我们进一步提供理论分析，说明NADO的近似质量如何影响可控的生成结果。请注意，在整个过程中，我们把基础模型和序列级oracle作为黑箱函数，不需要任何重构或微调。

现有的一些可控生成工作（例如Lu等人（2021））为词汇约束设计了解码算法。然而，他们的方法是纯算法的，一般不能应用于其他类型的口令。另一线工作，如PPLM（Dathathri等人，2020）、GeDI（Krause等人，2021）和FUDGE（Yang和Klein，2021）也旨在用一个辅助模型来指导基础模型。然而，它们要么以一种事后的方式改变基础模型的分布，而没有理论上的保证，要么/和需要外部标记的数据来训练辅助模型。相反，我们为纳入oracle的最佳方式推导出一个闭合式的解决方案，而不需要外部标记数据或标记级指导。此外，由于NADO是在基础模型采样的数据上训练的，所以它与基础模型的一致性更好，从而可以实现更好的控制。

我们对词汇约束生成（LCG）任务和机器翻译（MT）形式变化任务进行了实验。在LCG任务中，oracle是一个基于规则的关键词检查器。与之前设计特定解码算法的方法相比，我们实现了几乎完美的关键词整合，并大大提升了BLEU分数。在形式控制的MT任务中，我们提供了一个形式oracle，预测一个句子是否是正式的，目标是引导模型产生正式的翻译。与最近的工作Yang和Klein（2021）相比，我们将BLEU得分提高了3分，并提高了形式化率，证明了NADO在纳入外部oracle监督方面的卓越能力。两个实验都证明了我们的框架在处理各种类型的控制和生成高质量文本方面的有效性。

2 Related Work

Controllable Text Generation with Auto-regressive Models:以前大多数关于可控文本生成的工作都是基于自动回归框架的。Zhang等人（2022）将这些方法总结为三类：微调、重构/再训练和后处理。前两类，如CTRL（Keskar等人，2019）、提示方法（Shin等人，2020；Lester等人，2021；Li和Liang，2021），考虑到现在语言模型的规模正在急剧增加，通常控制力较弱，训练效率低下。一般来说，后处理方法被认为在推理方面很昂贵，而且生成的文本质量低。然而，我们的框架，作为一种后处理方法，能够实现实验中所证明的高生成质量，并且在推理时间上是高效的。

Controllable Text Generation via Post-processing:后处理有两条主线：（1）适应解码算法；（2）用辅助模型指导生成。对于一些token级控制的生成任务，如词汇约束生成，我们可以将约束注入到解码算法中（例如，约束束搜索（Anderson等人，2017）和NeuroLogic解码（Lu等人，2021））。虽然在词汇约束生成中显示出了有效性，但这些算法方法未能从根本上触及标记分布，也很难处理其他抽象属性。

在第二条线上，PPLM（Dathathri等人，2020）提出了一个用于指导模型的预期属性的辅助判别器；GeDi（Krause等人，2021）和DEXPERTS（Liu等人，2021）应用对比学习，训练一个辅助语言模型，在每个步骤中重新加权标记分布；Plug-and-Blend（Lin和Riedl，2021）通过添加一个规划器架构进一步扩展了GeDi框架。FUDGE（Yang和Klein，2021）利用外部token级oracle来训练一个用于指导基础模型的判别器。这些方法要么需要外部token级oracle指导，要么需要辅助标记的数据集来训练辅助模型。然而，用于训练辅助模型的数据的分布与基础模型的训练是不同的。这种分布上的差异导致了生成质量的下降，我们将在实验中展示。例如，给定一个控制属性a，Fudge根据贝叶斯规则$P(y_i|\textbf{y}_{<i},a)\propto P(a|\textbf{y}\leq i)P(y_{i}|\textbf{y}_{<i})$生成下一个token $y_i$。然而，他们的$P(a|\textbf{y}\leq i)$和$P(y_i|\textbf{y}_{<i})$并不是基于相同的分布来估计的。相比之下，NADO是用从基础模型采样的数据进行训练的。因此，它学会了与基础模型相结合，这就避免了分布上的差异。我们还提供了一个原则性的理论框架来讨论纳入序列级oracle的最佳解决方案。

3.Methodology

我们通过将句子级oracle分解为token级引导来处理序列级可控生成问题。我们将其表述为一个优化问题。由于token级指导是难以解决的，我们建议训练一个辅助模型，称为神经分解oracle（NADO），以近似它。在推理过程中，NADO指导基础模型生成满足oracle约束的序列。

在本节的其余部分，我们将讨论：

• 1）将序列级oracle函数分解为token级引导的表述。
• 2）将token级引导纳入基础模型以实现控制的表述。
• 3）使用NADO对token级引导进行近似。
• 4）从理论上分析NADO近似对可控生成结果的影响。
• 5）NADO的训练。

3.1 Notations and Problem Formulation

我们用$\textbf{x}{\in}\mathcal{X}$表示输入，$\textbf{y}{\in}\mathcal{Y}$表示生成的序列。$y_i$是$\textbf{y}$中的第$i$个标记，$\textbf{y}_{<i}$是从开始到第$(i-1)$个标记的序列前缀。我们将基本的自动回归生成模型表示为$p(y_i |\textbf{x},\textbf{y}_{<i})$，因此序列级分布由$p(\textbf{y}|\textbf{x})=\prod_{i}p(y_i|\textbf{x},\textbf{y}_{<i})$给出。序列级oracle被定义为一个布尔函数$C:\mathcal{X}{\times}\mathcal{Y}{\rightarrow}\{0,1\}$。我们将基于后验正则的优化目标正式化（Ganchev等人，2010）。我们探索一个token级分布$q^*(y_i|\textbf{x},\textbf{y}_{<i})$及其相应的序列级分布$q^*(\textbf{y}|\textbf{x})$，以满足

• 1. $q^*(\textbf{y}|\textbf{x})=\prod_i q^*(y_i|\textbf{x},\textbf{y}_{<i})$，即$q^*$可以作为一个自回归模型来处理。
• 2. $q^*(\textbf{y}|\textbf{x})=0 \ \text{if}\ C(\textbf{x},\textbf{y})=0$，即$q^*$仅可以生成满足oracle $C$的序列。
• 3. 给定一个输入$\textbf{x}$，$\text{KL}(p(\textbf{y}|\textbf{x})||q^*(\textbf{y}|\textbf{x}))$最小化，也就是说，$q^*$应该尽可能与基础模型相似。

3.2 Token-level Guidance and Closed-Form Solution For $q^*$

在我们计算$q^∗$的解决方案之前，鉴于基础模型$p$和oracle $C$，我们首先将token级引导定义为成功率预测函数$R_p^C(\textbf{x})$，它定义了$p$生成的序列满足oracle的概率，给定输入$\textbf{x}$。我们进一步定义$R^C_p(\textbf{x},\textbf{y}_{<i})$为给定输入$\textbf{x}$和前缀$\textbf{y}_{<i}$的概率。根据定义，我们有

$$\begin{equation} \begin{aligned} R_p^C(\textbf{x})=\text{Pr}_{\textbf{y}\sim p(\textbf{y}|\textbf{x})}[C(\textbf{x},\textbf{y})=1]=\sum_{\textbf{y}{\in}\mathcal{Y}}p(\textbf{y}|\textbf{x})C(\textbf{x},\textbf{y})\\ R_p^C(\textbf{x},\textbf{y}_{<i})=\text{Pr}_{\textbf{y}\sim p(\textbf{y}|\textbf{x})}[C(\textbf{x},\textbf{y})=1|\textbf{y}_{<i}]=\sum_{\textbf{y}{\in}\mathcal{Y}}p(\textbf{y}|\textbf{y}_{<i})C(\textbf{x},\textbf{y}) \end{aligned} \end{equation}$$

有了函数$R^{C}_{p}$，考虑到第3.1节定义的条件（2）和（3），我们现在能够推导出$q^*$的闭式解。给定输入$\textbf{x}$，我们定义可行的序列级分布集$Q$为

$$\begin{equation} \begin{aligned} Q\coloneqq\{q|\sum_{\textbf{q}:C(\textbf{x},\textbf{y})}q(\textbf{y}|\textbf{x})=0\} \end{aligned} \end{equation}$$

那么$q^*$的序列级闭式解就由以下公式给出:

$$\begin{equation} \begin{aligned} q^*(\textbf{y}|\textbf{x})=\mathop{\arg\min}_{q{\in Q}}\text{KL}(p(\textbf{y}|\textbf{x})||q(\textbf{y}|\textbf{x}))=\frac{p(\textbf{y}|\textbf{x})C(\textbf{x},\textbf{y})}{R_{p}^{C}(\textbf{X})} \end{aligned} \end{equation}$$

考虑到条件（1）并使$q^∗$具有可操作性，我们将$q^*(\textbf{y}|\textbf{x})$分解为token级。封闭式解法是由以下公式给出的

$$\begin{equation} \begin{aligned} q^*(y_i|\textbf{x},\textbf{y}_{<i})=\frac{R^C_p(\textbf{x},\textbf{y}_{<i})}{R_{p}^C(\textbf{x},\textbf{y}_{<i-1})}p(y_i|\textbf{x},\textbf{y}_{<i}) \end{aligned} \end{equation}$$

分解是唯一的。证明和详细推导可在附录中找到。

Control with Soft Constraints:在公式（2）中，我们将可行的分布集定义为序列违反oracle函数的可能性为0的分布。然而，在某些应用中，我们希望用软约束来控制生成。例如，我们希望该模型能以$r=0.8$的概率生成关于体育的句子。我们的框架也支持用软约束来控制生成。为了实现这一点，在预先定义的比率$r{\in}[0,1]$的情况下，我们可以选择定义一个一般的可行集$Q$为

$$\begin{equation} \begin{aligned} Q\coloneqq\{q|\sum_{\textbf{q}:C(\textbf{x},\textbf{y})}q(\textbf{y}|\textbf{x})=r\} \end{aligned} \end{equation}$$

其中，公式（2）是$r=0$时的特殊情况。 一般的token级闭式解是

$$\begin{aligned} q^*(y_i|\textbf{x},\textbf{y}_{<i})=\frac{\alpha R^{C}_{p}(\textbf{x},\textbf{y}_{<i})+\beta(1-R^C_p(\textbf{x},\textbf{y}_{<i}))}{\alpha R^{C}_{p}(\textbf{x},\textbf{y}_{<i-1})+\beta(1-R^C_p(\textbf{x},\textbf{y}_{<i-1}))}p(y_i|\textbf{x},\textbf{y}_{<i}) \end{aligned}$$

其中$\alpha=\frac{r}{R^C_p(\textbf{x})}$，$\beta=\frac{1-r}{1-R_p^{C}(\textbf{x})}$.

与公式（4）类似，一旦我们获得了$R^C_p$，我们就可以直接计算出闭式解，尽管其形式要复杂得多。在本文中，我们只关注硬约束（$r=0$），然而，在这里我们证明了我们的框架能够用于宽松的控制。

3.3 Approximating $R_p^C$ by NADO and Theoretical Analysis

不幸的是，公式（1）中定义的函数$R^C_p$是难以实现的。我们不能列举所有可能的序列y，因为空间是指数级的大。因此，我们训练一个神经模型NADO来近似这个定义明确的函数。我们用$R_\theta$表示NADO的参数化的$\theta$。在这一节中，我们推导出边界，对近似的误差和相应的序列级分布的误差之间的相关性进行理论分析。一般来说，当$R_\theta$足够精确地逼近$R_p^C$时，我们对序列级分布的差异有一个上限。下面的定理提供了正式的定义。

Lemma1: 我们定义分布

$$\begin{equation} \begin{aligned} q(y_i|\textbf{x},\textbf{y}_{<i}) \propto \frac{R_{\theta}(\textbf{x},\textbf{y}_{<i})}{R_\theta(\textbf{x},\textbf{y}_{i-1})}p(y_i|\textbf{x},\textbf{y}_{<i}). \end{aligned} \end{equation}$$

如果存在$\delta>1$，使得给定输入$\textbf{x},\forall\textbf{y}_{<i},\frac{1}{\delta}<\frac{R_\theta(\textbf{x},\textbf{y}_{<i})}{R_p^C(\textbf{x},\textbf{y}_{<i>})}<\delta$，我们有

$$\begin{aligned} \text{KL}(q^*(\textbf{y}|\textbf{x})||q(\textbf{y},\textbf{x}))<(2L+2)\ln\delta \end{aligned}$$

如果R也满足公式（6），我们可以收紧这个约束。从形式上看,

Lemma2:鉴于lemma1中的条件，如果$q$自然是一个没有归一化的有效分布（即$\sum_{y_i}\frac{R_{\theta}(\textbf{x},\textbf{y}_{<i})}{R_\theta(\textbf{x},\textbf{y}_{i-1})}p(y_i|\textbf{x},\textbf{y}_{<i})=1$），我们有

$$\begin{aligned} \forall\ x,\text{KL}(q^*(\textbf{y}|\textbf{x})||q(\textbf{y},\textbf{x}))<2\ln\delta \end{aligned}$$

这个定理表明，在自动回归特性下，误差不会随着序列的变化而累积。证明在附录中。这两个界限表明，在模型$R$的训练中，我们应该推动$R_\theta$满足公式（6）以及近似$R_p^C$。

3.4 Training NADO

在图1b中，我们展示了NADO的结构。一般来说，NADO可以是任何seq2seq模型。在训练中，它把$\textbf{x},\textbf{y}$作为输入，从$R_\theta(\textbf{x},\textbf{y}_{<0})$到$R_\theta(\textbf{x},\textbf{y}_{<T})$进行预测。在推理中，有两个平行的前向传递(在实践中，为了避免枚举词汇，$R_\theta$输出一个超过词汇的向量（即$R_\theta(\textbf{x},\textbf{y}_{<i} \bigoplus y)$，适用于所有可能的$y$，$\bigoplus$是连接操作），那么我们可以直接在$R_\theta$和$p$之间做元素相乘。)来计算token分布$q$。考虑到NADO的解码器大小通常远小于基础模型，整个前向传递不超过$2{\times}$基础模型前向传递。

3.5 Sampling

在第3.4节中，我们描述了我们通过对基础模型$p$的采样数据来训练NADO。一个优点是我们能够利用不同的采样策略来更好地适应不同的应用场景。也可以利用强化学习来训练$R_\theta$，我们在附录中讨论了我们与强化学习的联系。在这一节中，我们将介绍两种抽样策略和它们相应的属性。

Sampling with Temperature Control:在一些任务中，输出序列的变化不大，换句话说，每一步的标记分布是非常峰值的。由于我们的NADO是在抽样的例子上训练的，我们希望这些例子尽可能多地覆盖标记组合，以避免过度拟合。因此，我们添加温度系数$T$来平滑分布（Ackley等人，1985）。具体来说，我们从分布$p(\textbf{y}|\textbf{x})^{\frac{1}{T}}$中对$\textbf{y}$进行采样，并在计算交叉熵损失时加入系数$p(\textbf{y}|\textbf{x})^{1-\frac{1}{T}}$。形式上，预期损失为

$$\begin{aligned} \mathbb{E}_{\textbf{y}\sim p(textbf{y}|\textbf{x})^{\frac{1}{T}}}=[p(\textbf{y}|\textbf{x})^{1-\frac{1}{T}L_{CE}(\textbf{x},\textbf{y},R_{\theta})}]=\sum_{\textbf{y}{\in}\mathcal{Y}}p(\textbf{y}|\textbf{x})L_{CE}(\textbf{x},\textbf{y},R_{\theta}) \end{aligned}$$

这与公式（7）中的原始预期损失相同。

Importance Sampling:在实践中，当基础模型$p$生成的样本很难满足$C$时，NADO的训练过程会异常困难，即$\mathbb{E}_{\textbf{y}\sim p(\textbf{y}|\textbf{x})}[p(C|\textbf{x},\textbf{y})]\simeq 0$。因此，我们引入了重要性采样（Hammersley and Morton, 1954）来解决这个问题。我们利用现有的部分训练的$\hat{R}_{\theta}$来形成分布$\hat{q}$。虽然$\hat{R}_\theta$没有经过良好的训练，但它仍然能够提供积极的指导，以产生满足$C$的样本。注意，$\hat{q}$不需要在每个训练epoch更新。有了系数$\frac{p(\textbf{y}|\textbf{x})}{\hat{q}(\textbf{y}|\textbf{x})}$，预期损失与原始预期损失相同。

$$\begin{aligned} \mathbb{E}_{\textbf{y}\sim \hat{q}(textbf{y}|\textbf{x})}[\frac{p(\textbf{y}|\textbf{x})}{\hat{q}(\textbf{y}|\textbf{x})}L_{CE}(\textbf{x},\textbf{y},R_{\theta})] =\sum_{\textbf{y}\in\mathcal{Y}}p(\textbf{y}|\textbf{x})L_{CE}(\textbf{x},\textbf{y},R_{\theta}) \end{aligned}$$